Traduction d’un article de Hal Finney [1] publié en 1993 dans la dixième édition d’Extropy, le « journal de la pensée transhumaniste » [2]. Comment pouvons-nous défendre notre vie privée à l’ère de l’informatisation croissante ? Aujourd’hui, nos vies sont soumises à plusieurs sortes de surveillances. Chaque transaction par carte de crédit est enregistrée dans une base de données. Nos appels téléphoniques sont enregistrés par la compagnie de téléphone et utilisés à ses propres fins marketing. Nos chèques sont photocopiés et archivés par les banques. Et les nouvelles techniques de « matching » combinent les informations provenant de plusieurs bases de données, révélant encore plus de détails sur nos vies. À mesure que les bases de
Topics:
Jean-Luc considers the following as important:
This could be interesting, too:
Bitcoin Schweiz News writes Das ist das Crypto Builders Gathering in St. Moritz: Der Treffpunkt für die Zukunft der Krypto-Technologien
Wayne Jones writes Bad News for Crypto? Elizabeth Warren to Succeed Sherrod Brown on House Banking Committee
Martin Young writes Ethereum’s Modular Strategy: Short-Term Pain, Long-Term Gain, Says Research
Dimitar Dzhondzhorov writes 4 Reasons Why Bitcoin’s (BTC) Price Might See a Short-Term Correction
Traduction d’un article de Hal Finney [1] publié en 1993 dans la dixième édition d’Extropy, le « journal de la pensée transhumaniste » [2].
Comment pouvons-nous défendre notre vie privée à l’ère de l’informatisation croissante ? Aujourd’hui, nos vies sont soumises à plusieurs sortes de surveillances. Chaque transaction par carte de crédit est enregistrée dans une base de données. Nos appels téléphoniques sont enregistrés par la compagnie de téléphone et utilisés à ses propres fins marketing. Nos chèques sont photocopiés et archivés par les banques. Et les nouvelles techniques de « matching » combinent les informations provenant de plusieurs bases de données, révélant encore plus de détails sur nos vies. À mesure que les bases de données informatiques se développent et que de plus en plus de transactions ont lieu par voie électronique, via des systèmes téléphoniques et des réseaux informatiques, les formes possibles de surveillance croissent avec elles.
Comme on pouvait s’y attendre, la plupart des solutions proposées à ce problème impliquent davantage d’administration. Une solution consiste à adopter un ensemble de lois destinées à restreindre l’utilisation des informations : « Aucune information ne doit être utilisée à des fins différentes de celle pour laquelle elle a été initialement collectée. » Ainsi, les données sur les revenus collectées par une banque via le suivi de l’activité des comptes courants ne pouvaient pas être mises à la disposition des sociétés de listes de diffusion ; les enregistrements téléphoniques ne pouvaient pas être vendus aux agences de télémarketing, etc.
Mais c’est une mauvaise solution, pour de nombreuses raisons. Le gouvernement est notoirement inefficace dans l’application des lois existantes, et la facilité de collecte et d’utilisation des informations suggère qu’il serait presque impossible de faire appliquer avec succès une loi comme celle-ci. Le gouvernement a également tendance à s’exonérer de ses propres lois. Il est peu probable que l’IRS, par exemple, abandonne volontiers l’utilisation de la comparaison de bases de données qu’il utilise pour traquer les fraudeurs fiscaux. Et, bien sûr, l’idée même de tenter de restreindre l’utilisation de l’information nécessite des restrictions strictes sur les actions privées des individus, ce que les extropiens trouveront inacceptables.
Mais il existe une autre solution, défendue avec force par l’informaticien David Chaum du Centre de mathématiques et d’informatique aux Pays-Bas. Alors que la plupart des personnes concernées par ce problème se tournent vers des solutions gouvernementales paternalistes, Chaum a tranquillement mis en place les bases techniques d’une nouvelle façon d’organiser nos informations financières et personnelles. Plutôt que de compter sur de nouvelles lois et plus de gouvernement, Chaum se tourne vers des solutions techniques. Et ces solutions s’appuient sur une science ancienne vouée à la confidentialité des informations : la cryptographie.
La cryptographie, l’art de l’écriture secrète, a connu une révolution au cours des deux dernières décennies, révolution déclenchée par l’invention de la cryptographie à « clé publique ». S’appuyant sur cette nouvelle technologie, les informaticiens se sont diversifiés dans des dizaines de directions, repoussant les frontières du secret et de la confidentialité vers de nouveaux territoires. Et ce sont ces nouvelles applications de la cryptographie qui sont si prometteuses pour éviter les dangers décrits ci-dessus.
L’approche de Chaum en matière de protection de la vie privée peut être considérée comme comportant trois niveaux. La première couche est la cryptographie à clé publique, qui protège la confidentialité des messages individuels. La deuxième couche est la messagerie anonyme, qui permet aux personnes de communiquer par courrier électronique (« email ») sans révéler leur véritable identité. Et le troisième niveau est la monnaie électronique, qui permet aux gens non seulement de communiquer, mais aussi d’effectuer des transactions commerciales via un réseau informatique, avec le même type de confidentialité que celle dont vous bénéficiez lorsque vous utilisez de l’argent liquide. Si vous entrez dans un magasin aujourd’hui et effectuez un achat en espèces, aucune trace ne vous lie personnellement à la transaction. Sans enregistrements, il n’y a rien à introduire dans une base de données informatique. L’objectif de la monnaie électronique est de permettre que ces mêmes types de transactions privées s’effectuent par voie électronique.
(Sachez qu’il existe d’autres propositions de monnaie électronique qui ne protègent pas autant la vie privée des individus. Les propositions de Chaum visent à préserver les attributs de confidentialité de l’argent liquide, l’expression « monnaie numérique » est donc approprié. Mais d’autres solutions électroniques de remplacement de l’argent liquide non seulement manquent de confidentialité, mais faciliteraient en réalité la surveillance informatique en insérant des informations plus détaillées dans des bases de données et en décourageant l’utilisation d’espèces. Si vous voyez une proposition pour un système de monnaie électronique, vérifiez s’il a la capacité de préserver la confidentialité des transactions financières comme le fait le papier-monnaie aujourd’hui. Sinon, sachez que la proposition est conçue pour nuire, et non pour aider, à la vie privée des individus.)
Cryptographie à clé publique
La première des trois couches d’un système de monnaie électronique protégeant la vie privée est la cryptographie à clé publique. Le concept de base de la cryptographie à clé publique, inventé en 1976 par Diffie et Hellman, est simple. Les cryptographes décrivent traditionnellement un système de chiffrement comme étant composé de deux parties : une méthode de chiffrement et une clé. La méthode de cryptage est supposée être accessible au public, mais la clé reste secrète. Si deux personnes souhaitent communiquer, elles se mettent d’accord sur une clé secrète et l’utilisent pour crypter et déchiffrer le message.
La cryptographie à clé publique a introduit l’idée qu’il pouvait y avoir deux clés plutôt qu’une. Une clé, la clé publique, est connue de tous et est utilisée pour chiffrer les messages. L’autre clé, la clé secrète, n’est connue que de vous et est utilisée pour déchiffrer les messages. Les clés publiques et secrètes sont créées par paires, chaque clé publique correspondant à une clé secrète, et vice versa.
Ainsi, pour utiliser un système à clé publique, vous créez d’abord une paire de clés publique/secrète. Vous communiquez à tous vos amis votre clé publique, tout en gardant pour vous votre clé secrète. Lorsqu’ils souhaitent vous envoyer un message, ils le chiffrent à l’aide de votre clé publique. Le message crypté résultant n’est lisible qu’en utilisant votre clé secrète. Cela signifie que même la personne qui a crypté le message ne peut pas le déchiffrer ! S’il oublie le contenu de son message original, et qu’il l’a supprimé, il n’a aucune chance de reconstruire l’original. Vous seul pouvez le faire. C’est le paradoxe de la cryptographie à clé publique : une personne peut transformer un message de telle manière qu’elle ne peut inverser le processus, même si elle connaît la formule exacte utilisée pour effectuer la transformation.
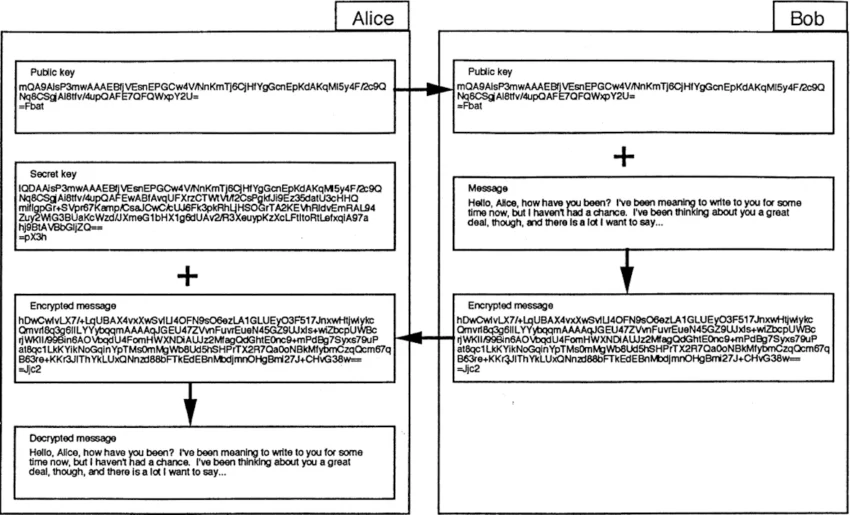
La figure 1 illustre les étapes impliquées dans l’utilisation d’un système à clé publique. (Les clés et les messages sont basés sur les résultats réels du programme libre de clés publiques de Phillip Zimmermann, PGP.) Alice, à gauche, crée d’abord une paire de clés publique et secrète, les deux cases supérieures de ce côté. Elle envoie la clé publique à son ami Bob, à droite. La deuxième case à gauche est la clé secrète, qu’Alice garde privée. Bob, à droite, reçoit et sauvegarde la clé publique d’Alice. Puis, lorsqu’il souhaite lui écrire, il compose un message, affiché dans la deuxième case de ce côté. Avec un programme de chiffrement à clé publique comme PGP, il chiffre le message en utilisant la clé publique d’Alice, produisant le résultat qui apparait dans la troisième case à droite.
Ce message chiffré est ce qu’il envoie à Alice, comme le montre la flèche menant vers la gauche. Alice utilise sa clé secrète enregistrée pour déchiffrer le message de Bob, lui permettant de reconstruire le message original de Bob, affiché dans la dernière case sur le côté gauche.
Il n’est plus nécessaire que la cryptographie à clé publique soit mystérieuse. Il existe désormais des logiciels du domaine public qui vous permettront d’expérimenter la cryptographie à clé publique sur votre propre ordinateur, notamment le PGP de Zimmermann et d’autres.
Messages anonymes
La cryptographie à clé publique permet aux personnes de communiquer électroniquement en toute confidentialité et sécurité. Vous pouvez envoyer des messages à l’abri des regards indiscrets grâce à ces techniques. Mais ce n’est qu’un pas vers la solution aux problèmes de confidentialité auxquels nous sommes confrontés. L’étape suivante fournit le deuxième niveau de confidentialité : les messages anonymes – les messages dont la source et la destination ne peuvent être retracées.
Cela est nécessaire en raison de l’objectif consistant à assurer dans un réseau électronique la confidentialité d’une transaction en espèces ordinaire. Tout comme un commerçant acceptera de l’argent liquide d’un client sans exiger de preuve d’identité, nous souhaitons également que notre système de monnaie électronique permette des transactions similaires, sans que l’identité des personnes impliquées ne soit révélée les unes aux autres, ni même à quelqu’un qui surveille le réseau.
Il existe des problèmes liés à la fourniture de messages anonymes dans les systèmes de messagerie actuels. Les réseaux nationaux de courrier électronique sont composés de milliers de machines, interconnectées via diverses passerelles et systèmes de transmission de messages. La nécessité fondamentale pour qu’un message soit délivré dans un tel système est qu’il soit adressé de manière appropriée. Généralement, une adresse e-mail se compose du nom d’un utilisateur et du nom du système informatique qui est sa « maison » électronique. Au fur et à mesure que le message circule sur le réseau, des informations de routage y sont ajoutées afin de conserver une trace de la provenance du message et des machines qu’il a traversées en route vers sa destination. Dans ce système, tous les messages sont clairement indiqués avec leur source et leur destination. Fournir des messages anonymes dans un tel système semble à première vue impossible.
Chaum a proposé deux systèmes distincts pour surmonter ce problème. Je me concentrerai ici sur ce qu’il appelle un « Mix » car plus simple et plus approprié pour l’application du courrier électronique anonyme.
La notion de Mix est simple. Il s’agit essentiellement d’un service de transfert de messages. Une analogie avec le courrier papier ordinaire peut être utile. Imaginez que vous vouliez envoyer une lettre à un ami, mais de telle manière que même quelqu’un qui surveille votre courrier sortant ne sache pas que vous faites cela. Une solution serait de mettre votre lettre dans une enveloppe adressée à votre ami, puis de placer cette enveloppe dans une enveloppe plus grande que vous enverriez à quelqu’un d’autre, accompagnée d’une note lui demandant de transmettre la lettre à votre ami. Cela cacherait la véritable destination de votre courrier à quelqu’un qui surveillait vos enveloppes sortantes.
Les Mix de Chaum utilisent cette idée de base, mais appliquée au courrier électronique et améliorée avec la cryptographie à clé publique. Un Mix est un programme informatique capable de recevoir du courrier électronique. Il reçoit des messages contenant des demandes de remailing vers une autre adresse, supprime simplement ces instructions de remailing et transfère les messages comme demandé. Chaum ajoute de la sécurité en ayant une clé publique différente pour chaque mix. Désormais, au lieu de simplement envoyer le message avec sa demande de transfert, le message ainsi que les informations de transfert sont cryptés avec la clé publique du Mix avant d’être envoyés au Mix. Le Mix décrypte simplement le message entrant avec sa clé secrète, révélant les informations de transfert, et envoie le message.
Pour protéger la vie privée de l’expéditeur, le Mix supprime les informations sur l’expéditeur d’origine du message avant de l’envoyer. Pour encore plus de sécurité, il est possible à l’expéditeur d’origine de spécifier une « Cascade » de Mix, toute une chaîne de Mix que le message doit parcourir avant d’être finalement envoyé à destination. De cette façon, même si l’un des mix est corrompu, il ne peut pas déterminer qui envoie à qui.
En utilisant des Mix, les exigences de base en matière de courrier anonyme sont donc remplies. Un message en route dans le réseau n’a pas besoin de révéler sa source et sa destination. Cela peut provenir d’un mix, aller vers un mix, ou une combinaison de ceux-ci.
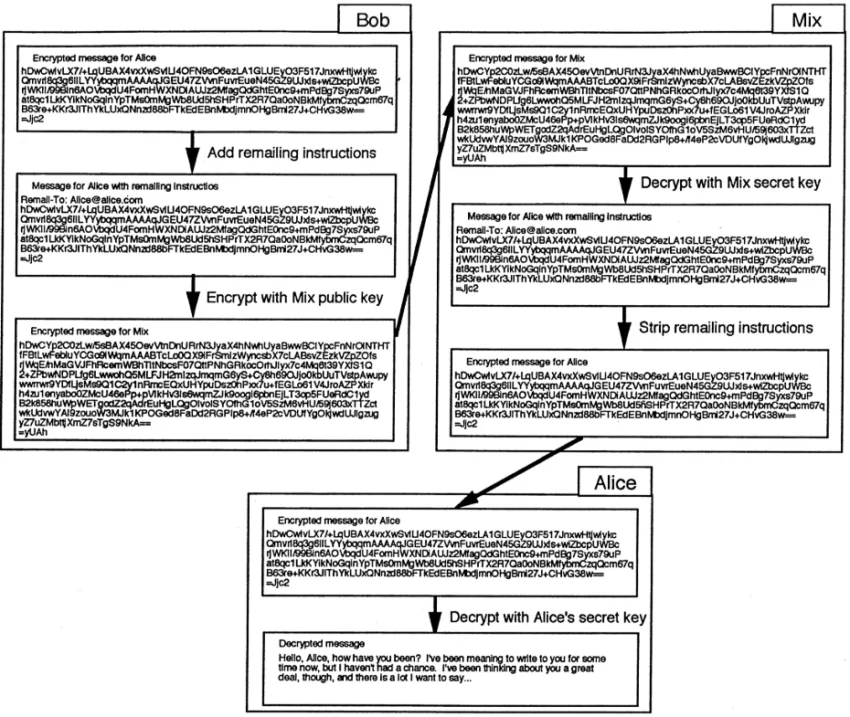
La figure 2 montre un exemple de message anonyme transmis via un Mix, utilisant la cryptographie à clé publique pour protéger sa confidentialité. Comme dans la figure 1, Bob souhaite envoyer son message crypté à Alice, mais cette fois il souhaite utiliser un Mix pour assurer plus de confidentialité. En commençant par le message chiffré de la figure 1, Bob (à gauche, cette fois) ajoute d’abord des instructions de repostage qui seront interprétées par le Mix. Ceux-ci incluront l’adresse e-mail d’Alice dans un format spécifié par le Mix. (Cet exemple utilise une forme simplifiée de commandes actuellement utilisées dans les remailers expérimentaux.) Ensuite, il crypte l’intégralité du message avec la clé publique du Mix et l’envoie au Mix.
Dès réception, le Mix inverse les étapes appliquées par Bob. Il déchiffre le message à l’aide de sa propre clé secrète, puis supprime les instructions de repostage ajoutées par Bob. Le message résultant (que le Mix ne peut pas lire, étant crypté à l’aide de la clé secrète d’Alice) est ensuite transmis à Alice comme spécifié dans les instructions de repostage. Comme auparavant, Alice reçoit et déchiffre le message grâce à sa clé secrète. Mais cette fois, le chemin du message a été protégé par le Mix, et le fait qu’Alice et Bob communiquent reste confidentiel.
Adresses de retour anonymes
Nous avons cependant besoin de quelque chose de plus avancé que l’anonymat des messages pour une messagerie véritablement privée. Ces messages anonymes sont essentiellement « à sens unique ». Je peux vous envoyer un message, avec la source et la destination cachées, et lorsque vous recevrez le message, vous n’aurez aucun moyen de savoir qui l’a envoyé. Cela signifie que vous ne pouvez pas me répondre. Nous avons besoin de pouvoir obtenir de telles réponses.
Nous avons ici une exigence en apparence paradoxale : pouvoir répondre à quelqu’un sans savoir ni qui il est ni quelle est son adresse email. Chaum montre comment ce problème peut être résolu en utilisant la cryptographie à clé publique et les mix. L’idée de base est ce que Chaum appelle une adresse de retour anonyme (ARA). Dans sa forme la plus simple, je crée un ARA en prenant mon adresse e-mail habituelle et en la chiffrant avec la clé publique d’un Mix particulier – appelez-le MixA pour cet exemple. Je vous envoie ce bloc de texte crypté résultant avec mon message, via une cascade de mélanges.
Désormais, lorsque vous recevez le message, vous ne voyez aucune adresse de retour, mais vous voyez le bloc de texte qu’est l’ARA. Vous pouvez me répondre sans savoir qui je suis en renvoyant votre réponse à MixA, accompagnée de l’ARA elle-même. MixA décrypte l’ARA à l’aide de sa clé secrète, récupérant ainsi mon adresse e-mail d’origine que j’ai chiffrée. Grâce à cette adresse e-mail, il est capable de me transmettre le courrier. J’ai pu recevoir ce message de votre part, même si vous n’avez aucune connaissance de ma véritable identité.
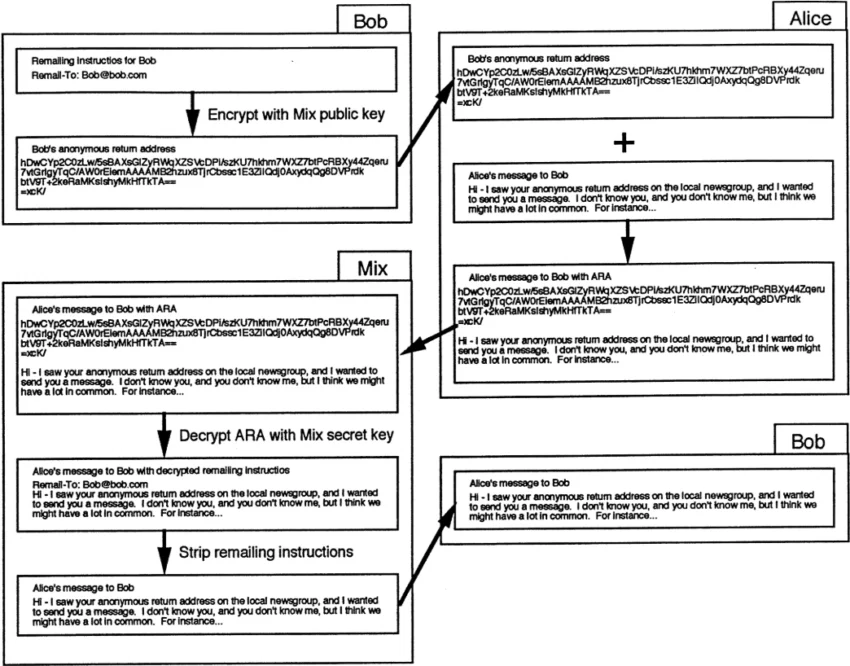
La figure 3 montre ce processus graphiquement. Bob, en haut à gauche, crée son ARA en chiffrant une commande de remailing, similaire à celle utilisée dans la figure 2, avec la clé publique du Mix. Il inclut ensuite cet ARA dans les messages qu’il envoie de manière anonyme ou qu’il publie publiquement. Dans l’exemple, Alice voit l’ARA de Bob et souhaite lui répondre, même si elle ne connaît pas son adresse email. Elle compose son message, dans la deuxième case à droite, puis combine son message avec l’ARA de Bob. Le message combiné est envoyé au Mix. Le Mix utilise désormais sa clé secrète pour déchiffrer la partie ARA du message, révélant les instructions de repostage que Bob a chiffrées pour créer l’ARA. Le reste du processus se déroule comme dans la figure 3. Le Mix supprime la demande de repostage et transfère le message à l’adresse de Bob, comme indiqué.
Ces outils ouvrent de nombreuses possibilités. Avec les Mix, les Cascades et les ARA, les gens peuvent communiquer sans connaître la véritable identité des autres. Vous pouvez publier un texte anonyme sur un forum public, inclure votre ARA et recevoir des réponses de nombreuses personnes qui ne savent pas qui vous êtes. Certains d’entre eux peuvent répondre de manière anonyme et inclure leurs propres ARA. Les gens peuvent finir par communiquer entre eux sans qu’aucun d’entre eux ne connaisse la véritable identité des autres.
(Certains systèmes de « Chat » ou de « « « simulateur de CB » offrent aujourd’hui l’illusion d’une telle communication anonyme, mais dans la plupart des cas, les opérateurs du système peuvent facilement percer le voile des identifiants et des pseudonymes et découvrir de véritables identités. Avec une Cascade de Mix, aucun Mix peut établir cette relation. Tant qu’un seul Mix de la Cascade reste intact, votre identité est en sécurité.)
Pseudonymes numériques
Les messages anonymes mettent en avant l’utilité des « pseudonymes numériques », un autre concept de Chaum. Sans identification de la source des messages, il semble impossible de vérifier que deux messages proviennent de la même personne. Il pourrait y avoir un problème avec des imposteurs se faisant passer pour d’autres personnes, ce qui entraînerait une confusion totale. Pour résoudre ce problème, nous avons besoin d’un autre concept issu de la cryptographie à clé publique : la « signature numérique ».
Comme décrit ci-dessus, la cryptographie à clé publique permet de déchiffrer les messages chiffrés avec ma clé publique avec ma clé secrète. Cependant, cela fonctionne également dans l’autre sens. Les messages peuvent être chiffrés avec ma clé secrète puis déchiffrés uniquement avec ma clé publique. Cette propriété est utilisée pour implémenter la signature numérique. Si je chiffre un document avec ma clé secrète, n’importe qui peut le déchiffrer avec ma clé publique. Et comme ma clé secrète est secrète, moi seul peux faire ce type de cryptage. Cela signifie que si un document peut être déchiffré avec ma clé publique, alors moi, et moi seul, dois l’avoir crypté avec ma clé secrète. Ceci est considéré comme une signature numérique, dans le sens où c’est une preuve que c’est moi qui ai « signé » (c’est-à-dire chiffré) le document.
Le concept de signature numérique peut être utilisé pour résoudre le problème de l’imposteur en autorisant les « pseudonymes numériques ». Mon pseudonyme numérique est simplement une paire de clés publique/secrète, dont je laisse connaître la partie publique. En règle générale, je la ferais connaître avec mon ARA. Désormais, pour prouver qu’un message donné vient de moi et de personne d’autre, je signe le message en utilisant la clé secrète de mon pseudonyme numérique. Tout ensemble de messages signés par ce même pseudonyme numérique est donc connu comme provenant de moi, car moi seul en connais la clé secrète. Les gens ne savent peut-être pas qui je suis, mais je peux toujours maintenir une personnalité publique stable sur les réseaux informatiques grâce à mon pseudonyme numérique. Et il n’y a aucun danger que quelqu’un d’autre réussisse à se faire passer pour moi.
Avec la cryptographie à clé publique, les Mix et les pseudonymes numériques, nous disposons de tout ce dont nous avons besoin pour créer un réseau d’entités communiquant de manière privée et anonyme. Mais à présent nous avons besoin d’un moyen pour que ces entités puissent faire des affaires tout en maintenant ces conditions.
Monnaie électronique
La prochaine étape, la troisième couche de notre description, est la monnaie numérique – la monnaie électronique. L’argent liquide, ordinaire papier-monnaie pliable, est l’un des derniers bastions de la vie privée dans notre vie financière. Et bon nombre des problèmes décrits ci-dessus – la perte de la vie privée, l’augmentation du nombre d’informations informatisées – pourraient être évités si l’argent liquide pouvait être utilisé plus facilement. Mais l’argent liquide présente de nombreux inconvénients. Il peut être perdu ou volé, et il dangereux de le transporter en grande quantité. De plus, il est inutilisable pour les achats effectués par voie électronique, par téléphone ou (à l’avenir) sur les réseaux informatiques. L’argent numérique est conçu pour combiner les avantages des systèmes de paiement électronique – la sécurité et la commodité – avec les avantages du papier-monnaie – la confidentialité et l’anonymat.
Une fois de plus, nous sommes confrontés à des paradoxes dans la notion de monnaie numérique. Étant donné que la monnaie numérique peut être envoyé par courrier électronique et par d’autres méthodes électroniques, il doit s’agir essentiellement d’un modèle d’information – en termes concrets, d’un modèle de lettres et de chiffres. Comment une telle chaîne de caractères pourrait-elle avoir une valeur, au même titre que le billet d’un dollar dans votre portefeuille ? Et la contrefaçon ? Une autre copie de la chaîne de caractères ne pourrait-elle pas être créée de manière triviale ? Qu’est-ce qui empêche une personne de dépenser deux fois le même argent ?
Pour répondre à ces questions, nous nous tournons à nouveau vers la cryptographie à clé publique. Sachez cependant que la monnaie électronique est un domaine de recherche actif en cryptographie. De nombreuses personnes ont proposé différents systèmes de monnaie électronique, chacun présentant ses propres avantages et inconvénients. Je présenterai ici un concept simplifié pour donner une idée des problèmes et des solutions qui existent.
Une façon de penser à la monnaie numérique est de faire une analogie avec les débuts du papier-monnaie. À une époque, le papier-monnaie n’était pas le monopole des gouvernements comme c’est le cas aujourd’hui. Le papier-monnaie c’était des « billets de banque » au sens littéral, souvent donnés comme reçus contre un dépôt d’or ou de monnaie « réelle » déposée dans les coffres des banques. Ces billets porteraient une description de leur valeur, par exemple « échangeable contre une once d’or ». Un billet de banque particulier pourrait être remboursé auprès de la banque émettrice pour sa valeur nominale. Les gens utilisaient ces billets de banque comme nous utilisons le papier-monnaie aujourd’hui. Ils étaient précieux car ils étaient soutenus par des matériaux de valeur dans les coffres-forts des banques.
En un certain sens, un billet de banque peut donc être considéré comme un document signé, une promesse d’effectuer un remboursement pour le porteur qui le présente à la banque. Cela suggère une façon de penser la monnaie numérique. Au lieu d’une note papier portant une signature, nous utiliserions plutôt un message électronique avec une signature numérique.
Une banque électronique pourrait, comme les banques d’autrefois, détenir des documents de valeur dans ses coffres. Aujourd’hui, il s’agirait probablement de dollars ou d’une autre monnaie gouvernementale, mais il pourrait s’agir d’or ou d’autres matières premières. En les utilisant comme support, elle émettrait des billets de banque. Il s’agirait de messages électroniques, signés numériquement par la clé secrète de la banque, promettant de transférer une somme spécifiée sur le compte de celui qui présenterait le billet à la banque (ou, si on le souhaite, de racheter le billet en dollars ou en d’autres objets de valeur.)
Voici comment cela pourrait fonctionner. Vous ouvrez un compte dans une banque électronique et déposez de l’argent comme dans n’importe quelle banque. La banque crédite ensuite votre compte de votre solde initial. Supposons maintenant que vous vouliez m’effectuer un paiement électronique. Avant toute transaction, vous enverriez un message à la banque, demandant un ou plusieurs billets de banque dans des coupures spécifiées. (C’est exactement la même chose que retirer de l’argent de votre compte bancaire habituel.) La banque débite votre compte, crée de nouveaux messages de billets de banque et vous les envoie. Ils vous sont envoyés sous forme de messages signés, cryptés avec la clé secrète de la banque. Lorsqu’il est déchiffré avec la clé publique de la banque, que tout le monde connaît, un billet de banque numérique d’un dollar indiquerait en effet : « Ce billet vaut 1,00 $, payable sur demande ». Il comprendrait également un numéro de série unique, comme celui d’un billet d’un dollar.
Le numéro de série est important ; comme nous le verrons ci-dessous, il est utilisé par la banque pour s’assurer qu’un billet particulier n’est accepté en dépôt qu’une seule fois. Mais apposer des numéros de série sur les billets de banque nuit à l’anonymat ; la banque peut se rappeler sur quel compte un billet de banque a été retiré, et lorsqu’il est déposé, la banque saura que le déposant fait affaire avec celui qui a reçu ce billet de la banque. Pour éviter cela, Chaum introduit une astuce mathématique astucieuse (trop complexe pour être décrite ici) qui permet de modifier aléatoirement le numéro de série au fur et à mesure que le billet est retiré de la banque. Le billet de banque conserve sa forme et sa valeur, mais le numéro de série est différent de celui que la banque a vu. Cela permet à la banque de vérifier que le même billet n’est pas déposé plus d’une fois, tout en rendant impossible pour la banque de déterminer qui a retiré un billet déposé.
Lorsque vous êtes prêt à acheter quelque chose chez moi, il vous suffit de m’envoyer par e-mail les messages de billets de banque appropriés. Je peux vérifier qu’il s’agit de billets de banque légitimes en utilisant la clé publique de la banque pour vérifier sa signature. J’envoie ensuite les billets par courrier électronique à la banque, qui vérifie que les numéros de compte figurant sur les billets n’ont pas été déposés auparavant. S’il s’agit de billets de banque valides, la banque crédite mon compte de la valeur nominale des billets. Votre compte a été diminué lorsque vous avez retiré les billets de banque que vous déteniez comme de l’argent liquide, et le mien a augmenté lorsque je les ai envoyés à la banque. Le résultat est similaire à la façon dont cela fonctionnerait si vous retiriez de l’argent (papier) de la banque, me l’envoyiez par courrier et que je déposais l’argent sur mon propre compte.
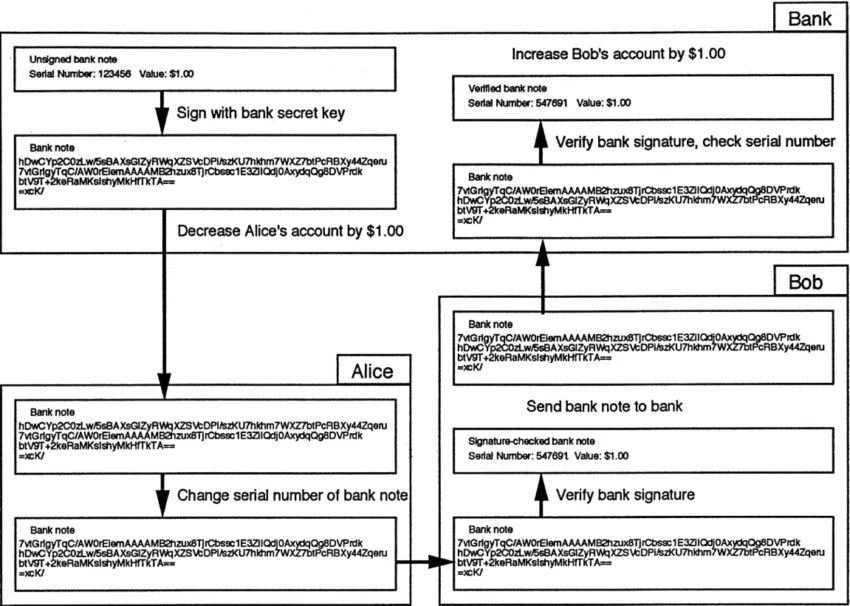
La figure 4 montre une transaction similaire entre Alice et Bob. La banque, dans le coin supérieur gauche, crée un billet de banque numérique en signant un message qui précise le numéro de série et la valeur du billet, et l’envoie à Alice. Alice, en le retirant, utilise la technique de Chaum pour modifier le numéro de série afin que la banque ne reconnaisse pas le billet comme provenant de ce retrait. Elle paie ensuite Bob par voie électronique en lui envoyant le billet de banque. Bob vérifie la validité du billet en le déchiffrant à l’aide de la clé publique de la banque pour vérifier sa signature. Il envoie ensuite le billet à la banque, qui vérifie le numéro de série pour confirmer que ce billet n’a pas été utilisé auparavant. Le numéro de série est différent de celui du retrait d’Alice, empêchant la banque de relier les deux transactions.
Avec cette simple image à l’esprit, nous pouvons commencer à répondre à certaines des objections énumérées ci-dessus. Les billets de banque ne peuvent pas être falsifiés car seule la banque connaît la clé secrète qui sert à les émettre. D’autres personnes ne pourront donc pas créer leurs propres billets de banque. Aussi, n’importe qui peut vérifier qu’un billet de banque n’est pas un faux en vérifiant la signature numérique de la banque sur le billet. Quant au problème de copie, qui empêche une personne de dépenser le même billet de banque plus d’une fois, il est résolu en vérifiant auprès de la banque si le numéro de série figurant sur le billet a déjà été utilisé avant d’accepter un billet de banque en guise de paiement. Si tel avait été le cas, la note ne serait pas acceptée. Toute tentative de réutilisation d’un billet de banque sera détectée car le numéro de série sera un double de celui utilisé précédemment. Cela signifie également qu’une fois que vous « dépensez » votre argent numérique en l’envoyant par courrier électronique à quelqu’un, vous devez le supprimer de votre ordinateur, car il n’aura plus aucune valeur pour vous.
Ce système simple donne un avant-goût de la monnaie électronique, mais il présente néanmoins des fonctionnalités délicates. La nécessité de vérifier auprès de la banque pour chaque transaction peut s’avérer gênante dans de nombreux environnements. Et la valeur fixe des billets de banque décrits ici, ainsi que l’impossibilité de les diviser en morceaux plus petits, limiteront également leur utilité. Chaum et d’autres ont proposé des systèmes plus complexes qui résolvent ces problèmes de différentes manières. Avec ces systèmes plus avancés, l’anonymat, la confidentialité et la commodité des transactions en espèces peuvent être obtenus même dans un environnement purement électronique.
La monnaie électronique en pratique
Après avoir décrit les trois niveaux de protection de la vie privée, nous pouvons maintenant voir comment les transactions électroniques peuvent préserver la vie privée des individus. La cryptographie à clé publique protège la confidentialité des messages et joue un rôle clé dans les autres couches. La messagerie anonyme permet en outre aux gens de communiquer sans en révéler plus sur eux-mêmes qu’ils ne le souhaitent. Et la monnaie électronique combine l’anonymat de l’argent liquide avec la commodité des paiements électroniques. David Chaum a décrit des variantes de ces techniques qui peuvent également étendre la protection de la vie privée à de nombreux autres domaines de notre vie.
Bien que ma description de l’argent numérique se fasse en termes de réseaux informatiques avec des transactions par courrier électronique, elle peut également être appliquée à une échelle plus locale. Avec des ordinateurs de la taille d’une carte de crédit, l’argent numérique pourrait tout aussi bien être utilisé pour payer des courses au supermarché local que pour commander des logiciels auprès d’un fournisseur anonyme sur les réseaux informatiques.
Les ordinateurs à « cartes à puce » utilisant l’argent numérique pourraient remplacer les cartes de crédit ou de débit à de nombreuses fins. Les mêmes types de messages seraient utilisés, l’interaction se faisant entre votre carte à puce et le lecteur de carte du commerçant.
Sur les réseaux eux-mêmes, tout bien ou service principalement basé sur l’information serait un candidat naturel pour les achats en espèces numériques. Aujourd’hui, cela peut inclure des éléments tels que des logiciels, des magazines électroniques et même des livres électroniques. À l’avenir, avec des réseaux à bande passante plus élevée, il sera peut-être possible d’acheter des enregistrements musicaux et vidéo sur Internet.
Comme autre exemple, la monnaie numérique et les réexpéditeurs anonymes (tels que les Mix de Chaum) entretiennent une relation synergique ; c’est-à-dire que chacun profite directement à l’autre. Sans réexpéditeurs anonymes, l’argent numérique serait inutile, car la confidentialité souhaitée serait perdue à chaque transaction, la source et la destination des messages étant clairement affichées dans les messages électroniques. Et dans l’autre sens, l’argent numérique peut être utilisé pour prendre en charge les services de repostage anonyme. Il pourrait y avoir une large gamme de services Mix disponibles sur les réseaux ; certains seraient gratuits et offriraient vraisemblablement des services relativement simples, mais d’autres seraient payants et offriraient plus de services ou des mesures de sécurité plus coûteuses. Ces entreprises de courrier à but lucratif pourraient être payées en espèces numériques.
Quelles sont les perspectives de mise en œuvre éventuelle des systèmes de paiement numérique et des autres technologies décrites ici ? Certaines expériences commencent déjà. David Chaum a créé une société, DigiCash, basée à Amsterdam, qui tente de mettre en place un système de monnaie électronique à petite échelle. Cependant, comme pour tout nouveau concept commercial, en particulier dans la communauté financière conservatrice, il faudra du temps avant qu’un nouveau système comme celui-ci soit largement utilisé.
Les nombreuses lois et réglementations couvrant les secteurs des services bancaires et financiers dans la plupart des pays occidentaux ralentiront sans aucun doute l’acceptation de l’argent numérique. Certains ont prédit que le succès initial de la monnaie électronique pourrait prendre la forme d’un « marché noir » techniquement illégal où les crypto-pirates achètent et vendent des informations, en utilisant la cryptographie pour se protéger contre les mesures répressives du gouvernement.
À plus court terme, les outils sont désormais en place pour permettre aux gens de commencer à expérimenter les autres concepts abordés ici. La cryptographie à clé publique devient une réalité sur les réseaux informatiques. Et des réexpéditeurs expérimentaux intégrant des systèmes de cryptographie à clé publique sont déjà utilisés à petite échelle. La publication de messages anonymes basés sur des pseudonymes numériques devrait commencer au cours de l’année prochaine. Le domaine évolue rapidement, alors que les défenseurs de la vie privée du monde entier se dépêchent de mettre en place ces systèmes avant que les gouvernements et autres grandes institutions puissent réagir.
Nous sommes aujourd’hui sur une voie qui, si rien ne change, mènera à un monde doté d’un potentiel de pouvoir, d’intrusion et de contrôle accrus des gouvernements. Nous pouvons changer cela ; ces technologies peuvent révolutionner les relations entre les individus et les organisations, en les mettant pour la première fois sur un pied d’égalité. La cryptographie peut rendre possible un monde dans lequel les gens contrôlent les informations les concernant, non pas parce que le gouvernement leur a accordé ce contrôle, mais parce qu’eux seuls possèdent les clés cryptographiques nécessaires pour révéler ces informations. C’est le monde que nous travaillons à créer.
Source : https://cdn.nakamotoinstitute.org/docs/protecting-privacy-with-electronic-cash.pdf
[1] Harold Thomas Finney dit Hal Finney (4 mai 1956 – 28 août 2014) était un développeur de la PGP Corporation. C’est également l’un des premiers utilisateurs de Bitcoin et le destinataire de la toute première transaction en BTC.
[2] Lancé par Max More et TO Morrow en août 1988, « Extropy : Journal of Transhumanist Thought » se présentait sous la forme d’un magazine imprimé. Dix-sept numéros ont été publiés entre 1988 et 1997.